Analyse du jeu de données de dureté Janka en Common Lisp
Table des matières
1 Introduction
Je montre ici comment le jeu de données de dureté Janka que nous avons analysé avec R peut-être analyser en Common Lisp. Je suppose que le lecteur possède quelques notions de Common Lisp (abrégé par la suite par CL). J'ai utilisé l'implémentation open source Steel Bank Common Lisp (SBCL, version 1.1.6). Le CL est un langage de programmation très complet et très puissant, mais comme c'est un langage « généraliste » (on peut réellement tout faire avec) il ne vient pas avec une sur-couche dédié aux applications en statistique, même si des bibliothèques ou paquet, existent pour certaines applications. Je vais donc avoir à coder beaucoup plus qu'avec R ; la décomposition QR va ainsi être codée explicitement et je vais utiliser directement ou adapté les codes que le lecteur pourra trouver sur le site Rosetta Code.
Je suppose que les données ont déjà été téléchargées, sinon, il suffira de taper en ligne de commande du shell :
wget http://www.uow.edu.au/~mwand/webspr/janka.txt
Je vais également utiliser la bibliothèque cl-csv qui peut-être simplement téléchargée, installée et chargée grâce à Quicklisp. Je commence donc par charger cl-csv :
(ql:quickload :cl-csv)
| :CL-CSV |
2 Chargement des données
Je commence par définir une fonction read-table qui nécessite la fonction read-csv du paquet cl-csv et qui va me permettre de charger le jeu de données dans mon espace de travail :
(defun read-table (file-path) "Loads file whose path is given in argument file-path and returns a list of list. The first sublist contains the namesof the columns while each subsequent sublist contains the individual observations." (let ((res (cl-csv:read-csv file-path :separator #\Tab))) (cons (car res) (mapcar #'(lambda (x) (list (read-from-string (nth 0 x)) (read-from-string (nth 1 x)))) (cdr res)))))
READ-TABLE
J'utilise ensuite la fonction pour charger les données :
(defparameter *janka* (read-table #P"janka.txt"))
*JANKA*
*janka*
| dens hardness | |
| 24.7 | 484 |
| 24.8 | 427 |
| 27.3 | 413 |
| 28.4 | 517 |
| 28.4 | 549 |
| 29.0 | 648 |
| 30.3 | 587 |
| 32.7 | 704 |
| 35.6 | 979 |
| 38.5 | 914 |
| 38.8 | 1070 |
| 39.3 | 1020 |
| 39.4 | 1210 |
| 39.9 | 989 |
| 40.3 | 1160 |
| 40.6 | 1010 |
| 40.7 | 1100 |
| 40.7 | 1130 |
| 42.9 | 1270 |
| 45.8 | 1180 |
| 46.9 | 1400 |
| 48.2 | 1760 |
| 51.5 | 1710 |
| 51.5 | 2010 |
| 53.4 | 1880 |
| 56.0 | 1980 |
| 56.5 | 1820 |
| 57.3 | 2020 |
| 57.6 | 1980 |
| 59.2 | 2310 |
| 59.8 | 1940 |
| 66.0 | 3260 |
| 67.4 | 2700 |
| 68.8 | 2890 |
| 69.1 | 2740 |
| 69.1 | 3140 |
(cdr *janka*)
| 24.7 | 484 |
| 24.8 | 427 |
| 27.3 | 413 |
| 28.4 | 517 |
| 28.4 | 549 |
| 29.0 | 648 |
| 30.3 | 587 |
| 32.7 | 704 |
| 35.6 | 979 |
| 38.5 | 914 |
| 38.8 | 1070 |
| 39.3 | 1020 |
| 39.4 | 1210 |
| 39.9 | 989 |
| 40.3 | 1160 |
| 40.6 | 1010 |
| 40.7 | 1100 |
| 40.7 | 1130 |
| 42.9 | 1270 |
| 45.8 | 1180 |
| 46.9 | 1400 |
| 48.2 | 1760 |
| 51.5 | 1710 |
| 51.5 | 2010 |
| 53.4 | 1880 |
| 56.0 | 1980 |
| 56.5 | 1820 |
| 57.3 | 2020 |
| 57.6 | 1980 |
| 59.2 | 2310 |
| 59.8 | 1940 |
| 66.0 | 3260 |
| 67.4 | 2700 |
| 68.8 | 2890 |
| 69.1 | 2740 |
| 69.1 | 3140 |
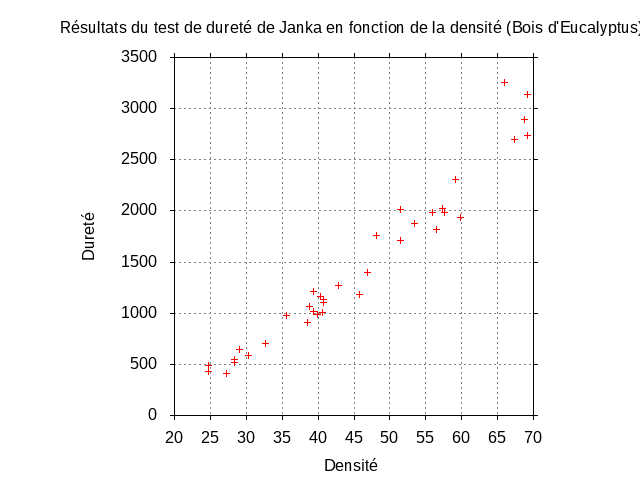
Le graphe en nuage de points de la dureté en fonction de la densité (fait avec gnuplot) est montré sur la figure \ref{fig:figure-janka-gnuplot}.
set title "Résultats du test de dureté de Janka en fonction de la densité (Bois d'Eucalyptus)" set xlabel "Densité" set xtics out set ylabel "Dureté" set ytics out set tics norotate nooffset set size square unset key set style line 12 lc rgb'#808080' lt 0 lw 1 set grid back ls 12 set style line 1 pointtype 3 linecolor "Blue" plot data using 1:2 with points
3 Définitions de fonctions « utilitaires »
Je définis dans cette section « un paquet » de fonctions pour :
- manipuler des matrices ;
- effectuer la décomposition QR ;
- effectuer une régression linéaire par la méthode des moindres carrés.
3.1 Manipulation de matrices
Tout d'abord la fonction element-wise-matrix :
(defun element-wise-matrix (fn A B) "Applies function fn, a function taking two arguments, element-wise to matrices A and B. No check is made that the matrices have the same dimensions. Matrices elements are accessed exploiting the row-major storage of arrays. A matrix with the dimensions of A is returned. So B could have more rows BUT THE SAME NUMBER OF COLUMNS than A and the result would still make sense." (let* ((len (array-total-size A)) (m (car (array-dimensions A))) (n (cadr (array-dimensions A))) (C (make-array `(,m ,n) :initial-element 0.0d0))) (loop for i from 0 to (1- len) do (setf (row-major-aref C i) (funcall fn (row-major-aref A i) (row-major-aref B i)))) C))
ELEMENT-WISE-MATRIX
Avec element-wise-matrix il est trivial de définir les fonctions :
m+, addition de matrices élément par élément ;m-, soustraction de matrices élément par élément ;m*, multiplication de matrices élément par élément ;m/, division de matrices élément par élément ;m^, exponentiation de matrices élément par élément.
(defun m+ (A B) (element-wise-matrix #'+ A B)) (defun m- (A B) (element-wise-matrix #'- A B)) (defun m* (A B) (element-wise-matrix #'* A B)) (defun m/ (A B) (element-wise-matrix #'/ A B)) (defun m^ (A B) (element-wise-matrix #'expt A B))
M^
Quelques exemples :
(m+ #2A((1 2) (3 4)) #2A((1 2) (3 4)))
#2A((2 4) (6 8))
(m- #2A((1 2) (3 4)) #2A((1 2) (3 4)))
#2A((0 0) (0 0))
(m* #2A((1 2) (3 4)) #2A((1 2) (3 4)))
#2A((1 4) (9 16))
(m/ #2A((1 2) (3 4)) #2A((1 2) (3 4)))
#2A((1 1) (1 1))
(m^ #2A((1 2) (3 4)) #2A((1 2) (3 4)))
#2A((1 4) (27 256))
Je définit la fonction element-wise-scalar qui applique une fonction arbitraire fn accepant deux arguments, à une matrice A et un scalaire c, élément par élément :
(defun element-wise-scalar (fn A c) "Applies function fn, a function taking two arguments, element-wise to matrix A and scalar c. A elements are accessed exploiting the row-major storage of arrays. A matrix with the dimensions of A is returned." (let* ((len (array-total-size A)) (m (car (array-dimensions A))) (n (cadr (array-dimensions A))) (B (make-array `(,m ,n) :initial-element 0.0d0))) (loop for i from 0 to (1- len) do (setf (row-major-aref B i) (funcall fn (row-major-aref A i) c))) B))
ELEMENT-WISE-SCALAR
Avec element-wise-scalar les fonctions suivantes sont immédiatement définies :
.+, addition d'une matrice et d'un scalaire ;.-, soustraction d'une matrice et d'un scalaire ;.*, multiplication d'une matrice et d'un scalaire ;./, division d'une matrice par un scalaire ;.^, exponentiation d'une matrice et d'un scalaire.
(defun .+ (A c) (element-wise-scalar #'+ A c)) (defun .- (A c) (element-wise-scalar #'- A c)) (defun .* (A c) (element-wise-scalar #'* A c)) (defun ./ (A c) (element-wise-scalar #'/ A c)) (defun .^ (A c) (element-wise-scalar #'expt A c))
\.^
Quelques exemples :
(.+ #2A((1 2) (3 4)) 5)
#2A((6 7) (8 9))
(.- #2A((1 2) (3 4)) 5)
#2A((-4 -3) (-2 -1))
(.* #2A((1 2) (3 4)) 5)
#2A((5 10) (15 20))
(./ #2A((1 2) (3 4)) 5)
#2A((1/5 2/5) (3/5 4/5))
(.^ #2A((1 2) (3 4)) 2)
#2A((1 4) (9 16))
La fonction mmul multiplie deux matrices au sens classique de la multiplication matricielle :
(defun mmul (A B) "Matrix multiplication of A by B." (let* ((m (car (array-dimensions A))) (n (cadr (array-dimensions A))) (l (cadr (array-dimensions B))) (C (make-array `(,m ,l) :initial-element 0))) (loop for i from 0 to (- m 1) do (loop for k from 0 to (- l 1) do (setf (aref C i k) (loop for j from 0 to (- n 1) sum (* (aref A i j) (aref B j k)))))) C))
MMUL
Exemple :
(mmul #2A((1 2) (3 4)) #2A((1 2 3) (4 5 6)))
#2A((9 12 15) (19 26 33))
La fonction mtp renvoie la transposée de son argument :
(defun mtp (A) "Returns the transpose matrix of its argument." (let* ((m (array-dimension A 0)) (n (array-dimension A 1)) (B (make-array `(,n ,m) :initial-element 0))) (loop for i from 0 below m do (loop for j from 0 below n do (setf (aref B j i) (aref A i j)))) B))
MTP
Exemple :
(mtp #2A((1 2 3) (4 5 6)))
#2A((1 4) (2 5) (3 6))
3.2 Décomposition QR
Fonction sign :
(defun sign (x) "Returns 0 is its argument x is 0, 1 if x > 0 and -1 otherwise." (if (zerop x) x (/ x (abs x))))
SIGN
Exemple :
(multiple-value-bind (a b c) (values (sign -5) (sign 0) (sign 13))
(list a b c))
| -1 | 0 | 1 |
La fonction norm renvoie la norme euclidienne de son argument qui doit être un vecteur colonne (une matrice à une colonne), si une matrice à plusieurs colonnes est passée en argument, la norme de sa première colonne est calculée :
(defun norm (x) "Returns the Euclidean norm of the column vector x or the norm of the first column of x if the latter is a matrix with several columns." (let ((len (car (array-dimensions x)))) (sqrt (loop for i from 0 to (1- len) sum (expt (aref x i 0) 2)))))
NORM
Exemple :
(- (norm #2A((1) (1) (1))) (sqrt 3))
0.0
La fonction make-unit-vector renvoie un vecteur colonne dont tous les éléments sont initialisés à 0 sauf le premier qui est initialisé à 1 :
(defun make-unit-vector (dim) "Returns a column vector with dim elements whose first element is 1 and all others are 0." (let ((vec (make-array `(,dim ,1) :initial-element 0.0d0))) (setf (aref vec 0 0) 1.0d0) vec))
MAKE-UNIT-VECTOR
Exemple :
(make-unit-vector 3)
#2A((1.0d0) (0.0d0) (0.0d0))
La fonction eye renvoie la matrice identité :
(defun eye (n) "Returns the nxn identity matrix." (let ((I (make-array `(,n ,n) :initial-element 0d0))) (loop for j from 0 to (- n 1) do (setf (aref I j j) 1.0d0)) I))
EYE
Exemple :
(eye 3)
#2A((1.0d0 0.0d0 0.0d0) (0.0d0 1.0d0 0.0d0) (0.0d0 0.0d0 1.0d0))
La fonction array-range renvoie une sous-matrice de son argument :
(defun array-range (A ma mb na nb) "Returns the submatrix of A between rows ma and mb and columns na and nb." (let* ((mm (1+ (- mb ma))) (nn (1+ (- nb na))) (B (make-array `(,mm ,nn) :initial-element 0.0d0))) (loop for i from 0 to (1- mm) do (loop for j from 0 to (1- nn) do (setf (aref B i j) (aref A (+ ma i) (+ na j))))) B))
ARRAY-RANGE
Exemple :
(array-range #2A((1 2 3) (4 5 6)) 1 1 1 2)
#2A((5 6))
Fonctions rows et cols renvoient respectivement le nombre de lignes et de colonne de leur argument :
(defun rows (A) (car (array-dimensions A))) (defun cols (A) (cadr (array-dimensions A)))
COLS
Exemples :
(rows #2A((1 2 3) (4 5 6)))
2
(cols #2A((1 2 3) (4 5 6)))
3
Les fonctions mcol et mrow extraient respectivement une colonne et une ligne d'une matrice et renvoient respectivement un vecteur ligne et un vecteur colonne :
(defun mcol (A n) "Extracts column n of matrix A and returns a column vector." (array-range A 0 (1- (rows A)) n n)) (defun mrow (A n) "Extracts row n of matrix A and returns a row vector." (array-range A n n 0 (1- (cols A))))
MROW
Exemples :
(mrow #2A((1 2 3) (4 5 6)) 0)
#2A((1 2 3))
(mcol #2A((1 2 3) (4 5 6)) 1)
#2A((2) (5))
La fonction array-embed remplace élément par élément les éléments de la matrice B (second argument) à ceux de A (premier argument) à partir de la row ième ligne (troisième argument) et de la col ième colonne (quatrième argument) de cette dernière ; la matrice résultante est renvoyée :
(defun array-embed (A B row col) "Replaces elements of A with the ones of B starting at row row and column col of A and returns the resulting matrix." (let* ((ma (rows A)) (na (cols A)) (mb (rows B)) (nb (cols B)) (C (make-array `(,ma ,na) :initial-element 0.0d0))) (loop for i from 0 to (1- ma) do (loop for j from 0 to (1- na) do (setf (aref C i j) (aref A i j)))) (loop for i from 0 to (1- mb) do (loop for j from 0 to (1- nb) do (setf (aref C (+ row i) (+ col j)) (aref B i j)))) C))
ARRAY-EMBED
Exemple :
(array-embed #2A((1 2 3) (4 5 6)) #2A((1 1) (1 1)) 0 1)
#2A((1 1 1) (4 1 1))
La fonction make-householder construit une matrice de Householder, nécessaire à la transformation de Householder, à partir de son argument, un vecteur colonne :
(defun make-householder (a) "Makes a Householder matrix out of column vector a and returns the result." (let* ((m (car (array-dimensions a))) (s (sign (aref a 0 0))) (e (make-unit-vector m)) (u (m+ a (.* e (* (norm a) s)))) (v (./ u (aref u 0 0))) (beta (/ 2 (expt (norm v) 2)))) (m- (eye m) (.* (mmul v (mtp v)) beta))))
MAKE-HOUSEHOLDER
Un test_:
(defparameter *matrice-test* #2A ((12 -51 4) (6 167 -68) (-4 24 -41)) "Matrice used as example on the wikipedia page.")
*MATRICE-TEST*
(mmul (make-householder (mcol *matrice-test* 0)) *matrice-test*)
#2A((-14.0d0 -21.00000000000001d0 14.0d0)
(-5.551115123125783d-17 173.92307692307693d0 -65.6923076923077d0)
(4.440892098500626d-16 19.38461538461538d0 -42.53846153846154d0))
La fonction qr effectue la décomposition QR de son argument et renvoie les matrices Q et R :
(defun qr (A) "Performs a QR decomposition of its argument A and returns Q and R." (let* ((m (car (array-dimensions A))) (n (cadr (array-dimensions A))) (Q (eye m))) ;; Work on n columns of A. (loop for i from 0 to (if (= m n) (- n 2) (- n 1)) do ;; Select the i-th submatrix. For i=0 this means the original matrix A. (let* ((B (array-range A i (1- m) i (1- n))) ;; Take the first column of the current submatrix B. (x (mcol B 0)) ;; Create the Householder matrix for the column and embed it into an mxm identity. (H (array-embed (eye m) (make-householder x) i i))) ;; The product of all H matrices from the right hand side is the orthogonal matrix Q. (setf Q (mmul Q H)) ;; The product of all H matrices with A from the LHS is the upper triangular matrix R. (setf A (mmul H A)))) ;; Return Q and R. (values Q A)))
QR
Un test
(multiple-value-bind (Q-test R-test) (qr *matrice-test*)
(list Q-test R-test))
(#2A((-0.8571428571428572d0 0.3942857142857143d0 0.33142857142857146d0)
(-0.4285714285714286d0 -0.9028571428571428d0 -0.03428571428571427d0)
(0.28571428571428575d0 -0.17142857142857137d0 0.9428571428571428d0))
#2A((-14.0d0 -21.00000000000001d0 14.0d0)
(5.9781239787508525d-18 -175.00000000000003d0 70.0d0)
(4.475052806950631d-16 0.0d0 -35.0d0)))
3.3 Régression linéaire
Je commence par définir la fonction solve-upper-triangular qui résoud un système triangulaire supérieur par back substitution (substitution rétrograde ?) :
(defun solve-upper-triangular (R b) "Solves Rx = b, where R is triangular superior by back substitution and returns x." (let* ((n (cadr (array-dimensions R))) (x (make-array `(,n 1) :initial-element 0.0d0))) (loop for k from (- n 1) downto 0 do (setf (aref x k 0) (/ (- (aref b k 0) (loop for j from (+ k 1) to (- n 1) sum (* (aref R k j) (aref x j 0)))) (aref R k k)))) x))
SOLVE-UPPER-TRIANGULAR
Puis la fonction lsqr qui prend comme premier argument la matrice X du plan d'expérience et comme second argument le vecteur d'observations Y :
(defun lsqr (X Y) "Solves the least square problem that is minimize ||Y-Xβ|| with respect to β which gets returned." (multiple-value-bind (Q R) (qr X) (let* ((n (cadr (array-dimensions R)))) (solve-upper-triangular (array-range R 0 (- n 1) 0 (- n 1)) (array-range (mmul (mtp Q) Y) 0 (- n 1) 0 0)))))
LSQR
Le test du site Rosetta Code :
(defun polyfit (x y n) (let* ((m (cadr (array-dimensions x))) (A (make-array `(,m ,(+ n 1)) :initial-element 0))) (loop for i from 0 to (- m 1) do (loop for j from 0 to n do (setf (aref A i j) (expt (aref x 0 i) j)))) (lsqr A (mtp y)))) (let ((x #2A((0 1 2 3 4 5 6 7 8 9 10))) (y #2A((1 6 17 34 57 86 121 162 209 262 321)))) (polyfit x y 2))
#2A((0.9999999663451051d0) (2.0000000151446935d0) (2.9999999987980406d0))
4 Ajustement des données
Maintenant que nous avons tout ce dont nous avons besoin, nous pouvons procéder à l'ajustement des données de façon similaire à ce que nous avons fait avec R.
4.1 Matrice \(\mathbf{X}\) du plan d'expérience
Comme avec l'approche « à la main » que nous avons employée avec R, nous commençons par créer notre matrice du plan d'expérience :
(defparameter *X* (let* ((n (1- (length *janka*))) (res (make-array `(,n 3) :initial-element 1.0d0))) (loop for i from 0 to (1- n) do (setf (aref res i 1) (car (nth (1+ i) *janka*))) (setf (aref res i 2) (expt (car (nth (1+ i) *janka*)) 2))) res) "Design matrix for the janka data set using an intercept, the density and the square density")
*X*
4.2 Décomposition QR
(defparameter *X-QR* (multiple-value-bind (Q R) (qr *X*) (list Q R)) "QR decomposition of *X*")
*X-QR*
On vérifie simplement que la matrice Q a la bonne dimension :
(array-dimensions (car *X-QR*))
| 36 | 36 |
Attention, a décomposition QR telle que nous l'avons codée est analogue à celle de Octave, c'est-à-dire que ses trois premières colonnes engendre le même sous-espace vectoriel que les colonnes de *X*. On vérifie maintenant qu'elle est orthogonale (en examinant ici les 5 première lignes et colonnes de la transposée de Q multipliée par Q) :
(array-range (mmul (mtp (car *X-QR*)) (car *X-QR*)) 0 4 0 4)
#2A((0.9999999999999993d0 -5.828670879282072d-16 -3.400058012914542d-16
-1.9499376072151797d-16 -1.9325903724554117d-16)
(-5.828670879282072d-16 0.9999999999999998d0 -2.7755575615628914d-16
-7.724940478959219d-17 -7.551468131361538d-17)
(-3.400058012914542d-16 -2.7755575615628914d-16 0.9999999999999999d0
-1.7433970933566911d-16 -1.717376241217039d-16)
(-1.9499376072151797d-16 -7.724940478959219d-17 -1.7433970933566911d-16
0.9999999999999996d0 -9.366257396677558d-17)
(-1.9325903724554117d-16 -7.551468131361538d-17 -1.717376241217039d-16
-9.366257396677558d-17 0.9999999999999997d0))
4.3 Estimateur des moindres carrés
(defparameter *Y* (let* ((n (1- (length *janka*))) (res (make-array `(,n 1) :initial-element 0.0d0))) (loop for i from 0 to (1- n) do (setf (aref res i 0) (cadr (nth (1+ i) *janka*)))) res) "Column vector of observed values (hardness) from the janka data set") (defparameter *β-chapeau* (lsqr *X* *Y*) "Estimated parameter of the least square fit of the hardness using an intercept, the density and the square density.") *β-chapeau*
#2A((-118.0072246809923d0) (9.434013697324879d0) (0.5090775528911596d0))
4.4 Tests d'adéquation
La première chose à faire à ce stade est de rajouter la courbe ajustée aux données sur une figure. On définit au préalable une fonction qui nous renvoie le domaine couvert par les colonnes d'une matrice :
(defun range (M col) "Returns a list with two elements, the min and the max of column col (second argument) of matrix M (first argument). " (do* ((n (car (array-dimensions M))) (min (aref M 0 col) (if (< (aref M i col) min) (aref M i col) min)) (max (aref M 0 col) (if (> (aref M i col) max) (aref M i col) max)) (i 1 (1+ i))) ((> i (1- n)) (list min max)))))
RANGE
Puis on calcule les prédictions du modèle sur une grille fine recouvrant les valeurs des variables prédictives :
(let* ((nstep 100) (domaine (range *X* 1)) (step (/ (- (cadr domaine) (car domaine)) nstep)) (dd (loop for d from (car domaine) to (cadr domaine) by step collect d)) (plan (make-array `(,(length dd) 3) :initial-element 1.0d0))) (loop for i from 0 to (1- (length dd)) do (setf (aref plan i 1) (nth i dd)) (setf (aref plan i 2) (expt (nth i dd) 2))) (let ((pred (mmul plan *β-chapeau*))) (loop for i from 0 to (1- (length dd)) collect (list (nth i dd) (aref pred i 0)))))
| 24.7 | 425.59605875539734d0 |
| 25.144001 | 441.05102473098304d0 |
| 25.588001 | 456.70671342334583d0 |
| 26.032001 | 472.56312483248576d0 |
| 26.476002 | 488.6202278867749d0 |
| 26.920002 | 504.87808472946915d0 |
| 27.364002 | 521.3366332173126d0 |
| 27.808002 | 537.9958733503053d0 |
| 28.252003 | 554.855867271703d0 |
| 28.696003 | 571.91655283825d0 |
| 29.140003 | 589.1779611215741d0 |
| 29.584003 | 606.6400921216753d0 |
| 30.028004 | 624.3029458385536d0 |
| 30.472004 | 642.1664912005812d0 |
| 30.916004 | 660.2307592793859d0 |
| 31.360004 | 678.4957500749678d0 |
| 31.804005 | 696.9614325156988d0 |
| 32.248005 | 715.627868744835d0 |
| 32.692005 | 734.4949966191202d0 |
| 33.136005 | 753.5628472101828d0 |
| 33.580006 | 772.8314205180225d0 |
| 34.024006 | 792.3006543993833d0 |
| 34.468006 | 811.9706731407772d0 |
| 34.912006 | 831.8413524556923d0 |
| 35.356007 | 851.9128166306407d0 |
| 35.800007 | 872.1849413791101d0 |
| 36.244007 | 892.6577888443567d0 |
| 36.688007 | 913.3313590263804d0 |
| 37.132008 | 934.2056519251812d0 |
| 37.576008 | 955.2806675407594d0 |
| 38.020008 | 976.5563437298587d0 |
| 38.46401 | 998.032804778991d0 |
| 38.90801 | 1019.7099264016445d0 |
| 39.35201 | 1041.5877707410752d0 |
| 39.79601 | 1063.6663377972832d0 |
| 40.24001 | 1085.9456275702682d0 |
| 40.68401 | 1108.4256400600302d0 |
| 41.12801 | 1131.1063752665698d0 |
| 41.57201 | 1153.9878331898863d0 |
| 42.01601 | 1177.069951686724d0 |
| 42.46001 | 1200.3528550435947d0 |
| 42.90401 | 1223.8364189739866d0 |
| 43.34801 | 1247.5207056211557d0 |
| 43.79201 | 1271.405714985102d0 |
| 44.23601 | 1295.4914470658255d0 |
| 44.68001 | 1319.777901863326d0 |
| 45.124012 | 1344.2650793776038d0 |
| 45.568012 | 1368.9529796086588d0 |
| 46.012012 | 1393.8414782699788d0 |
| 46.456013 | 1418.930823934588d0 |
| 46.900013 | 1444.2208923159744d0 |
| 47.344013 | 1469.711559127626d0 |
| 47.788013 | 1495.4030729425667d0 |
| 48.232014 | 1521.2951851877724d0 |
| 48.676014 | 1547.3880201497554d0 |
| 49.120014 | 1573.6817021150277d0 |
| 49.564014 | 1600.175982510565d0 |
| 50.008015 | 1626.8709856228795d0 |
| 50.452015 | 1653.7667114519713d0 |
| 50.896015 | 1680.8631599978398d0 |
| 51.340015 | 1708.1603312604861d0 |
| 51.784016 | 1735.6582252399091d0 |
| 52.228016 | 1763.3568419361093d0 |
| 52.672016 | 1791.2561813490868d0 |
| 53.116016 | 1819.3562434788414d0 |
| 53.560017 | 1847.6569040388613d0 |
| 54.004017 | 1876.1584116021702d0 |
| 54.448017 | 1904.860641882256d0 |
| 54.892017 | 1933.7634705926075d0 |
| 55.336018 | 1962.8671463062478d0 |
| 55.780018 | 1992.1714204501532d0 |
| 56.22402 | 2021.676417310836d0 |
| 56.66802 | 2051.382261174808d0 |
| 57.11202 | 2081.288703469045d0 |
| 57.55602 | 2111.395868480059d0 |
| 58.00002 | 2141.7037562078503d0 |
| 58.44402 | 2172.212366652419d0 |
| 58.88802 | 2202.9216998137645d0 |
| 59.33202 | 2233.8317556918873d0 |
| 59.77602 | 2264.942534286787d0 |
| 60.22002 | 2296.2540355984647d0 |
| 60.66402 | 2327.766135340407d0 |
| 61.10802 | 2359.4790820856383d0 |
| 61.55202 | 2391.3927515476466d0 |
| 61.99602 | 2423.5070194399204d0 |
| 62.44002 | 2455.8221343354835d0 |
| 62.88402 | 2488.3378476613116d0 |
| 63.328022 | 2521.0544079904284d0 |
| 63.772022 | 2553.9715667498112d0 |
| 64.21602 | 2587.0892879515523d0 |
| 64.66002 | 2620.407767857977d0 |
| 65.10402 | 2653.927094767691d0 |
| 65.54802 | 2687.647268680694d0 |
| 65.99202 | 2721.5680410239625d0 |
| 66.43602 | 2755.6894117974957d0 |
| 66.88002 | 2790.0116295743182d0 |
| 67.32402 | 2824.53469435443d0 |
| 67.76802 | 2859.2581089917826d0 |
| 68.21202 | 2894.1826192054486d0 |
| 68.65602 | 2929.3077278493793d0 |
Ce qui nous permet, avec gnuplot, d'obtenir la figure \ref{fig:figure-janka-modele1-gnuplot}.
set title "Dureté en fonction de la densité (Bois d'Eucalyptus)" set xlabel "Densité" set xtics out set ylabel "Dureté" set ytics out set tics norotate nooffset set size square unset key set style line 1 pointtype 3 linecolor "Blue" set style line 2 linecolor "Black" plot data using 1:2 with points, model using 1:2 with lines
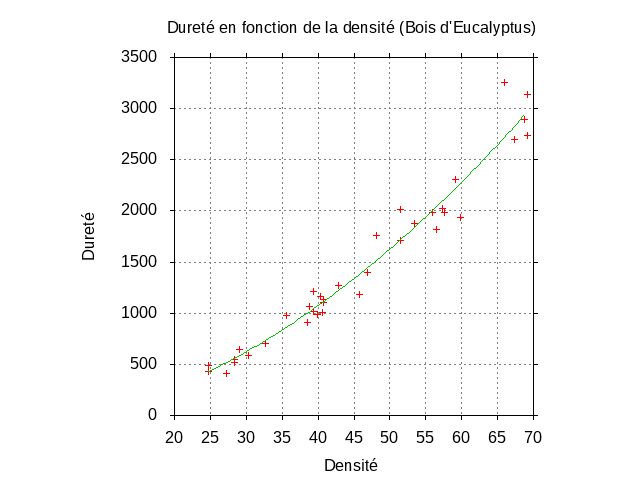
À ce stade aucune « pathologie majeure » n'est visible. Nous devons encore construire deux graphes obligatoires :
- les résidus, \(\hat{\mathbf{Z}} \equiv \mathbf{Y} - \mathbf{X} \, \hat{β}\) en fonction des valeurs ajustées ou prédites, \(\hat{\mathbf{Y}} \equiv \mathbf{X} \, \hat{β}\) ;
- un diagramme Quantile-Quantile avec les quantiles d'une loi normale centrée réduite en abscisse et les quantiles des résidus en ordonnée.
À suivre…